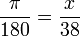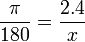GEOMETRIA

1. SEMEJANZA 1.1. Triángulos semejantes

En general, dos o más figuras son semejantes cuando tienen la misma forma pero no necesariamente el mismo tamaño. Esto aplica, lógicamente, a los triángulos.

El anterior concepto lo podríamos calificar como primario (intuitivo), y se complementa de formalidad al decir que cuando se establece la relación entre sus lados y ángulos se cumple que:

1. Los lados homólogos o correspondientes son proporcionales.

2. Los ángulos homólogos o correspondientes son congruentes.

EJERCICIO EN CLASES 

•  En las siguientes situaciones aplica  los requisitos de formalidad de la semejanza entre figuras planas. En las dos primeras verifica si son semejantes las parejas de triángulos y en la tercera halla la medida del lado OP asumiendo que los dos triángulos son semejantes.

SITUACION 1

SITUACION 2

SITUACION 3

ALGEBRA

UNIDAD 1     FRACCIONES ALGEBRAICAS                                                    

1. FRACCIONES ALGEBRAICAS

1.1. Concepto

•  Una fracción algebraica es una expresión fraccionaria en la que el numerador y el  denominador son polinomios. 
•  Es el cociente entre dos polinomios P(X)/Q(X), donde Q(X) es diferente de cero.

1.2. Simplificación de fracciones

                                   

                           

¡QUE SEA UN MOTIVO APRENDER DIBUJO TECNICO!

Bienvenidos estudiantes del Juan al mundo del Dibujo Técnico. Visualízate como un experto, desarrollando con habilidad y destreza sus  tareas de dibujante.

Una vez observados los videos podemos generar un foro de opiniones en el cual tu puedes participar.

¡ANIMATE!

 ¿Es necesario saber dibujar para iniciar este curso?

¡EVOLUCIONEMOS EN NUESTRA FORMA DE PENSAR!

Este espacio ha sido creado para que los actores de la Comunidad Juanista: padres de familia, docentes, directivos docentes, administrativos y estudiantes; reflexionemos sobre nuestros compromisos, evaluemos nuestras actuaciones frente a ellos y demos los saltos necesarios para evolucionar en nuestra forma de pensar.

COMO SUPERAR ALGUNOS CONFLICTOS INTRAFAMILIARES

TRIGONOMETRIA Y GEOMETRIA ANALITICA

UNIDAD 1  SISTEMAS DE MEDICION ANGULAR 1. ANGULOS Y SISTEMAS DE MEDICION

INTRODUCCION A LA TRIGONOMETRIA Y LA GEOMETRIA ANALITICA

La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Deriva de los términos griegos τριγωνο trigōno 'triángulo' y μετρον metron 'medida'.¹

En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno,coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión.

                   

TAREA:
1. Transcribir el alfabeto griego con el nombre de cada letra.
2.  Consultar sobre la historia de la trigonometría

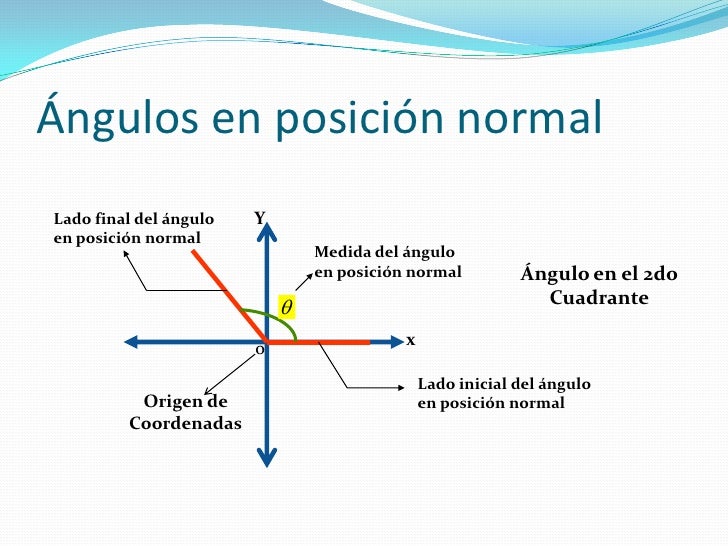
1.1. Angulo en posición normal

 

Concepto de ángulo en posición normal

Es aquel ángulo cuyo lado inicial coincide con el semieje positivo X y su vértice está localizado en el origen del plano cartesiano.

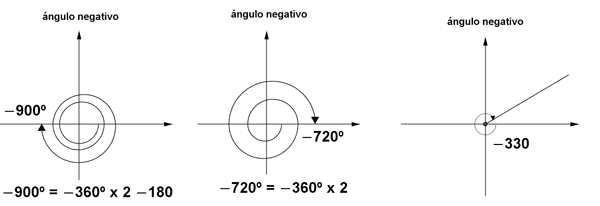
Angulos positivos y negativos

• Un ángulo es positivo cuando su lado final gira en sentido contrario a las manecillas del reloj.
• Un ángulo es negativo cuando su lado final gira en el mismo sentido de las manecillas del reloj.

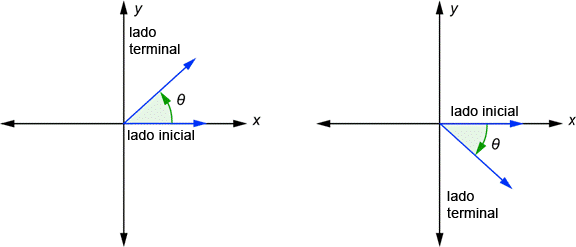Representación general de ángulos positivos (izq) y negativos (der)

Angulo cuadrantal

Un ángulo es cuadrantal cuando está en posición normal y su lado final coincide con algún semieje coordenado

1.2. Sistemas de medida angular 

• Medida de ángulos en el sistema sexagesimal

El sistema sexagesimal es aquel cuya unidad patrón es el Grado Sexagesimal (  °),
el cual se define como 1/360 parte de un giro completo.
                 
               

Ejercicio en clases

Dibujar en posición normal los siguientes ángulos: 36°, 0°, 1.028°, -45°, -132°, 4.780° 
Ejemplos:

"Para el aprendizaje efectivo de la matemática se necesita trabajar desde dos dimensiones, la teoría y la práctica, binomio indispensable para asegurar el éxito del mismo. La primera proporciona la visión y confianza, la segunda fija la seguridad y la experiencia para el dominio del curso"

 Prof. Abel Esteban Ortega Luna

• Medida de ángulos en el sistema cíclico

Este sistema utiliza como unidad fundamental el radián. El radián es el ángulo que se forma por un arco igual a la longitud del radio del círculo.

EJERCICIO EN CLASES

Traza una circunferencia de 4cm de radio y con  ayuda de un hilo, mide e indica en ella los ángulos: 3 rad, 4 rad, 1/2 rad, 5 rad, 2,5 rad

• Equivalencias entre el sistema sexagesimal y el sistema cíclico

Un ángulo de 360° equivale a 2π radianes; un ángulo de 180° equivale a π radianes (recordemos que el número π ≈ 3,14159265359…).

Para convertir grados en radianes o viceversa, partimos de que 180° equivalen a π radianes; luego planteamos una regla de tres y resolvemos.

Ejemplos:

1. Convertir 38° a radianes:

Primero planteamos la regla de tres. Nótese que la x va arriba, en la posición de los radianes.

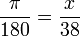
Despejamos x, también simplificamos.

Por último obtenemos el equivalente decimal:

x = 0,6632 radianes.

2. Convertir 2,4 radianes a grados.

Primero planteamos la regla de tres. Nótese que la x va abajo, en la posición de los grados.

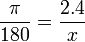
Despejamos x.

Por último obtenemos el equivalente decimal:

x = 137.5099°".

Nota: Tomado de Wikipedia, marzo 15 de 2.015

    
     GEOMETRIA

1. RECTAS EN EL PLANO